Binary To Gray Code And Gray To Binary Code
AIM: To realize 4-Bit Code Converter: Realization using XOR gates.
LEARNING OBJECTIVE:
- To learn to generate Gray To Binary
- To learn to generate Binary To Gray
COMPONENTS REQUIRED:
- IC 7486 X-OR GATE
- Patch Cords & IC Trainer Kit
- More Logic Gates Truth Table
THEORY:
Binary to Gray:
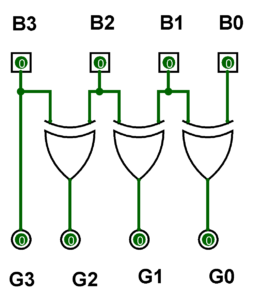
The 4 bit combination assigned to Binary Code to Gray. four bits to represent a decimal digit. There are four inputs and four outputs. The input variable are defined as B3, B2, B1, B0 and the output variables are defined as G3, G2, G1, G0. from the truth table, combinational circuit is designed.
B3 = G3
B2 ⊕ B3 = G2
B1 ⊕ B2 = G1
B0 ⊕ B1 = G0
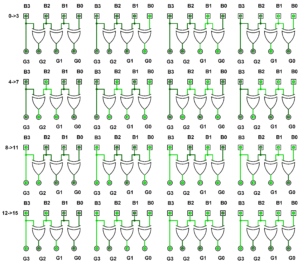
BINARY TO GRAY OUTPUT TRUTH TABLE
| Sno. | Binary Code | Gray Code | |||||||
| B3 | B2 | B1 | B0 | G3 | G2 | G1 | G0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | |
| 6 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 8 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | |
| 11 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 12 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 13 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 15 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
Gray to Binary:
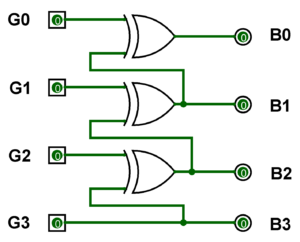
The 4 bit combination assigned to Gray to Binary Code. four bits to represent a decimal digit. There are four inputs and four outputs. The input variable are defined as G3, G2, G1, G0 and the output variables are defined as B3, B2, B1, B0. from the truth table, combinational circuit is designed.
G0 ⊕ G1 ⊕ G2 ⊕ G3 = B0
G1 ⊕ G2 ⊕ G3 = B1
G2 ⊕ G3 = B2
G3 = B3
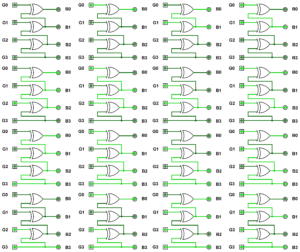
GRAY TO BINARY OUTPUT TRUTH TABLE
| Sno. | Gray Code | Binary Code | |||||||
| G3 | G2 | G1 | G0 | B3 | B2 | B1 | B0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 5 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | |
| 6 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 8 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 9 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 12 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | |
| 13 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 14 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 15 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
Very well explained